Zu diesem Thema gibt es umfangreiche Literatur, hier soll nur ein Einstieg in einige Teile der Mathematik geboten werden.
Mathematik lebt von der Beziehung von Zahlen zu und untereinander. Diese Beziehung nennt man Gleichungen, die einfachste ist 2 + 2 = 4.
Gleichungen sind gleich, wenn beide Seiten der Gleichung identisch (also austauschbar) sind!
Gleichungen können auch ungleich sein, dann sind diese Beziehungen durch Größer als (>) oder Kleiner als (<) ausgedrückt.
Lineare Gleichungen sind solche, die eine (oder mehrere) Unbekannte ohne Exponent enthalten, wie zum Beispiel später im Dreisatz zu sehen., Quadratische Gleichungen enthalten eine Variable mit Exponent.
Es gibt für diese Gleichungsysteme einige Grundregeln, die bei der Lösung der Gleichung zu beachten sind:
Eine Zahl wird dem Bruch zugerechnet, in dem man die Zahl mit dem Nenner multipliziert und zum Zähler addiert:
![]()
Eine Zahl wird vom Bruch abgezogen, in dem man die Zahl mit dem Nenner multipliziert und vom Zähler subtrahiert
![]()
Division eines Bruches durch eine Zahl:
![]()
![]()
Multiplikation eines Bruches mit einer Zahl
![]()
Addition von Brüchen
Brüche werden addiert (subtrahiert), in dem man den kleinsten
gemeinsamen Vielfachen der Nenner sucht und die einzelnen Zähler
mit dem Multiplikator aus dem einzelnen Nenner multipliziert. Dann
werden die einzelnen Brüche zu einem Bruch zusammengesetz und
die Zähler addiert (oder auch subtrahiert)![]()
![]()
![]()
hierbei
ist g:n=e und g:m=c
Findet sich kein KGN (Kleinster gemeinsamer
Nenner), so nimmt man das Produkt aus den Nennern
![]()
Multiplikation von Brüchen
Brüche
werden multipiziert, in dem man die Zähler und die Nenner
separat multipiziert
![]()
Division von Brüchen
Brüche werden dividiert, in dem
man mit dem Kehrwert multipliziert![]()
Man teilt durch einen Bruch, indem man mit seinem Kehrwert mal nimmt(also Zähler und Nenner tauscht)
ein wichtiges Instrument in der Mathematik zur Bestimmung von Schnittpunkten zweier Funktionen dh. Die Stelle an der das Ergebnis beider Funktionen in Abhängigkeit eines Wertes gleich wird, ist das sogenannte Gleichsetzungsverfahren.
Hierbei werden die beiden Funktionen (d.h. Gleichungen) direkt gleichgesetzt, und das ermittelte Ergebnis ist der Punkt, an dem diese Gleichungen ein gemeinsames Ergebnis haben.
Ein Beispiel hierzu:
y = 2x + 2 und y=3x
=> 2x + 2 = 3x
<=> 2=3x - 2x
<=> 2=(3-2)x
<=> 2=x
in eine der Gleichungen eingesetzt: y = 2*2 + 2 = 6
Kontrolle (andere Gleichung): y = 3*2 = 6
Ergebnis bei x=2 sind beide Gleichungen gleich 6 und somit erfüllt.
Eine sinnvolle Anwendung finden wir in der Andler-formel, also der Bestimmung der optimalen Bestellmenge:
![]()
Zu dieser Formel kommt man, wenn man die Einzelformeln für Lagerhaltungskosten Kl=m*p*q :2 und mittelbare Bestellkosten Km=B*Kf / m gleichsetzt. (Siehe Link)
Das Additionsverfahren ist eine weiter Möglichkeit, das Ergebnis für Gleichungen mit zwei Variablen zu lösen.
Beispiel:
a) 2x + 4y = 20 (* -2)
b) 4x + 10y = 8
a) (-4x) + (-8y) = -40
b) 4x + 10y = 8
=>[a)+b)] 10y - 8y = - 32
<=> 2y = - 32
<=> y = -16
Eingesetzt in Gleichung a): 2x + 4*(-16) = 20
2x - 64 =
20
2x = 84
x = 42
Kontrolle: x=42 in 4x + 10y = 8 => 4 * 42 + 10*(-16) =8
168
- 160 = 8
Wir hatten bereits vorausgesetzt, daß Gleichungen das Verhältnis von Zahlen oder Werten (Variablen) untereinander darstellen.
Dies führt ausserdem zum Begriff der Funktion: Gleichungen mit bekannten Zahlen, oder Variablen, die zu einem eindeutigen Ergebnis führen [z.B.: 2x+ 2 = 6 => x=2] nennt man Therm. Haben wir hingegen Gleichungen mit z.B. zwei Variablen, so ist dies bereits eine Funktion, die eine eindeutige Lösung nicht mehr zulassen [2x + 4 = y]; somit sind hier mehrere Zahlenkombinationen möglich, um diesen Therm aufzulösen [(0,4)(1,6)(2,8)(3,10)...] Diese Menge der Zahlen, die Zur Lösung dieser Gleichung führen nennt man Lösungsmenge der Funktion f(x)=2x+4 (Gesprochen f von x). Eine weitergehende Betrachtung des Funktionsbegriff, welche Formen und Arten von Funktionen es gibt, sprengt hier den Rahmen und ist nicht weiter interessant - Nur den Begriff als solchen sollte man zumindest schon gehört haben.
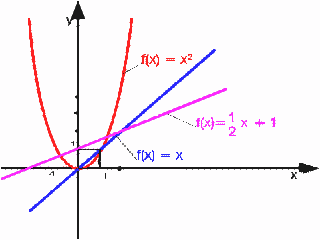
Die Darstellung der Funktion in einem Koordinatensystem nennt man Graph von f(x). Diese Kurve, Linie oder was auch immer wird durch die Wertepaare der Lösungsmenge gebildet, da einem Wert x auf der X-Achse (daher auch der Name) ein Lösungswert y [f(x)] auf der Y-Achse zugeordnet wird. Die Darstellung erzeugt dann eine geschlossene (wenige Ausnahmen, z.B. Tangens, ausgenommen) Linie.
Kleiner-Kleiner
Grösser-Grösser
Kleiner-Grösser
Grösser-Kleiner
A = B, C = x
A >(<) C, B >(<) x
dann folgt daraus: (B * C) / A = x
A = B, C = x
sei A < C und B > x
oder
A = B, C = x
sei A > C und B < x
dann folgt daraus: (A * B ) / C = x
werden errechnet, indem man die einzelenen Verhältnisse zum gesuchten Ergebnis sieht und einzeln in die Rechnung einbringt, d.h. aufschlüsselt und nacheinander auf den Bruch bringt.
Beispiel: 6 Kräne veladen 1200 tonnen in 7 Stunden auf 5 Schiffe; wieviel Stunden brauchen 10 Kräne um 800 Tonnen auf 8 Schiffe zu laden?
| 12(A)rbeiter | (*) |
12 (T)age | (*) |
8 h | 54 (E)inheiten | |
| (:) |
( :) |
(*) |
(:) |
|||
| 18 (A)rbeiter | 09 (T)age | x h | 81 (E)inheiten |
| x h = | 8 h * 81 E * 12 T * 12 A |
| 54 E * 9 T * 18 A |
Prozentrechnung gehört zu den elementarenRechenarten in der Wirtschaft, daher sollte man sie beherrschen. Jede Hochrechnung, die Verzinsung des Kapitals, der Wertverfall der Waren oder der Lagerzinssatz wird prozentual angegeben.
Begriffe: Grundwert G entspricht 100 %
Prozentsatz p ist der
Rechenfaktor in %, % entspricht dem Faktor 0,01
Prozentwert P
entspricht Grundwert G mal prozentsatz p[%] geteilt durch 100
Formeln: G * p /100 = P
P * 100 / p = G
p[%] = (P / G) *
100 [%]
Beispiel: Ein Meister verdient nach 6% Gehaltserhöhung EUR 2600,- . Wie hoch war sein Gehalt vor der Erhöhung?
P = 2600, p = 106 , G =100 P / p => G = 2600 * 100 / 106 = 2452,38
Warum ist p = 106? P ist größer als G, somit muss der Prozentsatz p über 100 liegen !
Beispiel: Ein Meister verdient EUR 2600,- Er muss 36% an den Fiskus abführen, es verbleiben ihm 64% seines Gehaltes. Wie hoch ist sein Nettoverdienst, wie hoch seine Abgaben?
G = 2600, p = 36 , P = G * p / 100 => P = 2600 * 0,36 = 936 (Abgaben)
G = 2600, p' = 64, P = G * p / 100 => P = 2600 * 0,64 = 2600 - 936 = 1664,- (Nettogehalt)
Beispiel: Ein Meister verdient EUR 2600,-. Er führt EUR 936,- monatlich an den Staat ab. Wie hoch ist sein Steuersatz, wenn der Sozialsatz allein bei 24 % liegt?
p [%] = 936/2600 * 100 [%] = 36 % (Gesamtabgaben) => 36% - 24% = 12% (Steuersatz)
.Voraussetzungen: Der Begriff Strecke, Der Begriff Höhe, Gleichungen, Variblen
 Ein Quadraht ist ein Rechteck,
bei dem die Seiten alle gleich lang sind und die Seiten einen rechten
Winkel bilden
Ein Quadraht ist ein Rechteck,
bei dem die Seiten alle gleich lang sind und die Seiten einen rechten
Winkel bilden
a
Seite a = Seite b => Fläche A =
a²; Umfang U = 4a
b Seite a # Seite b => Fläche A
= ab; Umfang U = 2 (a+b)
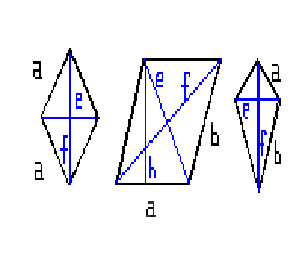
Ein
Viereck, bei dem ein Paar in der Seitelänge variiert und
wenigstens zwei Seiten keinen rechten Winkel bilden, die Diagonalen
sich halbieren(Raute und Parallelogramm) oder senkrecht zueinader
stehen (Raute und Drache)
Raute: A = ½ ef U = 4a
Parallelogramm: A = a h U = 2 (a+b)
Drachen: A = ½ ef U = 2 (a+b)
A = ½ (a+c) * h = m*h U=a+b+c+d wobei a und c parallel sind
Für alle Dreiecke gilt: Fläche = Grundseite mal Höhe
durch 2 also A = ½ c * h
Die Summe der Seiten ist der
Umfang, die Winkelsumme ist 180°
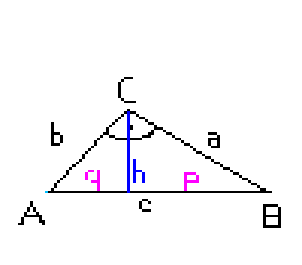 Rechtwinkliges
Dreieck:
Rechtwinkliges
Dreieck:
Satz des Pythagoras: a² + b² = c²
Kathetensatz: a² = cp ; b² = cq
Höhensatz: h² = pq
Fläche A = ½ c h = ½ a b (halbe Fläche des Rechtecks)
Umfang U = a + b + c
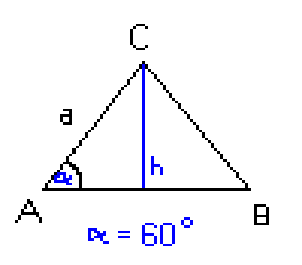 Gleichseitiges
(alle Winkel 60°) und Gleichschenkeliges Dreieck
Gleichseitiges
(alle Winkel 60°) und Gleichschenkeliges Dreieck
Gleichseitig: A=a²/4 Ö3 h = a/2 Ö3
Gleichschenkelig: A= ½ chc h = Ö a² -(c/2)²
Kreisfläche, Umfang und Segmente benötigen eine Konstante namens pi =3,1415926...
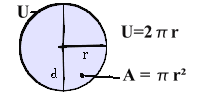 Kreisfläche A = p
r² = p
d²/4
Kreisfläche A = p
r² = p
d²/4
Grundsätzlich gilt hier: Man suche die geeignete Grundfläche in der Gesamtfläche, die einfach zu berechnen ist, um damit die Restflächen zu oder abrechnen zu können.
Beispiel: Ein Fachbodenregal soll mit Fächern ausgestattet werden, die einen runden Ausschnitt von d=20 cm zur Aufnahme von Rohren haben. Die einzelnen Fächer haben die Maße von 100 cm * 60 cm. Wie groß ist die verbliebene Stellfläche pro Fachboden?
Rechnung: Die Fläche des
Fachbodens errechnet sich durch A = a * b
=> A = 100 * 60 [cm
* cm] = 6000 cm²
Die Fläche des Kreisausschnittes errechnet sich durch A = 3,14159 (pi) * r²
=> A = 3,14159 * (20 cm / 2)² = 314 cm²
Also verbleibt an Gesamtfläche: 6000 cm² - 314 cm² = 5686 cm² = 0,5686 m²
Beispiel: Eine Lagerhalle mit der Breite von 20m und einer Länge von 60m ist in zwei Teile vom jeweils 30m unterteilt. Der erste Teil, der zur Lagerung von Paletten dient, soll durch Versatz der Wand in den hinteren Teil vergrößert werden. Bautechnisch ist diese Abteilung aber nur mit einem Winkel von 30° zur ursprünglichen Teilerwand und einem kürzesten Abstand von 9 m und einem längsten von 17m zu dieser Wand möglich.
Die Produktionswerkstatt im ehemalig rückwertigen Teil der Halle wird ausgelagert, um Verwaltungsbüros darin einzurichten. Somit wurde auch das ehemalige Büro des Lagerverwalters mit 12 m² aus der ersten Halle in diesen Teil verlegt.
Zusätzlich wird eine Verladerampe in eine Ecke des vorderen Teil eingebaut, wobei die LKW einen Einfahrtweg in die Halle von 4m Breite und 12m Länge haben, der mit der zusätzlichen Abtrennung von zwei 1,20 breiten Gehwegen um die Längskanten des tieferliegenden Einfahrtweges der Nutzung als Fläche nicht mehr zur Verfügung steht. Der Ladebereich an der Rampe geht in der Breite über die Stirnkante der Laderampe und der Breite der Gehwege und ragt 5m in die Halle hinein.
An der Rückwand der neuen Halle wurde zusätzlich ein runder Versorgungsschacht mit einen Durchmesser von 1,75 m in den Boden der Halle gebohrt, versehen mit einer Lochgitterplatte zur Abdeckung.
Diese Bereiche sind stets freizuhalten und stehen als Lagerfläche nicht mehr zur Verfügung.
Wie groß ist die neue Lagerfläche (Wegfall durch Gänge werden hierbei nicht berücksichtigt!)?
Der Verwalter des Lagers meint, dies sei ein Nachteil. Hat die Umbaumaßnahme mehr Lagerfläche geschaffen oder hat der Verwalter Recht?
a) 1.) 20m * 30m = 600 m² hatte die Lagerhalle ursprünglich,
abzüglich der 12m² des Büros, die nun hingegen wieder
hinzukommen.
2.) Durch den Versatz der Rückteilerwand um 9m
gewinnen wir 9m * 20m = 180 m² hinzu.
3.) Da die Wand nicht rechtwinklig, sondern um 30° nach hinten fliehend eingebaut wurde, erhalten wir ein angesetztes Dreieck hinzu. Wir kennen die Länge von 20m als Seite a und die Länge von (17 - 9) 8 m als Seite b eines rechtwinkligen Dreiecks. Daher ist die Flächenberechnung des Dreiecks:
20m * 8m /2 = 80m²
Somit erhalten wir eine neue Grundfläche von 600m² + 180m² + 80m² = 860m²
4.) Die Ladeeinfahrt mit einer Fläche von 4 m * 12 m = 48 m²
zusammen mit der Beladezone von: 6,4 m (4m Stirnfläche +
2*1,2 m Gehweg)* 5 m = 32 m²
und den seitlichen Gehwegen von
je 12m * 1,2m =14,4 m² also 28,8 m² Fläche fallen
jedoch wieder als Nutzfläche aus.
5.) Der Schacht mit 1,75 m Durchmesser hat eine Fläche von
3,14159 * (1,75 m)² /4 =3,14159*(0,875 m) ²=2,41 m².
Diese Fläche entfällt ebenfalls
Somit ist die neue Nutzfläche der Halle: 860m² - 48 m² - 32m² - 28,8 m² - 2,41m² = 748,79 m²
b) Somit hat auch der Verwalter unrecht, da dieser ursprünglich 600 m² - 12 m², also 588 m² zur Verfügung hatte.
Der bekannteste Körper ist der Würfel, gefolgt vom Bierglas (ich meine das zylindrische Altbierglas)
Warum aber weiß der Wirt, dass in das Glas 0,3 l Bier passen? Weils draufsteht! Aber woher wusste der Schreiber das? Der konnte rechnen, also wurde er nicht Wirt...sorry, kleiner Scherz am Rande...
Verschieden Körper haben einfache Formeln zur Errechnug des Rauminhaltes (Volumens). Hierbei ist ihnen eins gemein, nämlich das sich hier die Formel aus der Grundfläche mal der Höhe - G * h zusammensetzt.
Hierzu zählen der Würfel, der Zylinder, der Quader, das Prisma, (eigentlich auch Pyramiden- und Kegelstumpf)
Würfel (Gegenstück Quadrat): G*h = (a*a)*a = a³
Quader(Gegenstück Rechteck): G*h = (a*b)*c=a*b*c 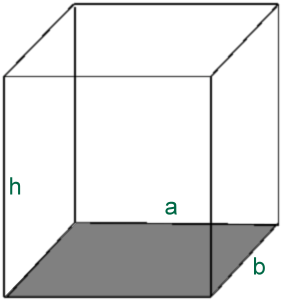
Prisma (Gegenstück Dreieck): G*h = (c*h)/2 * d = (c * h *d)/2
Zylinder (Gegenstück Kreis): G*h = (pi * r²) * h = pi
*r² *h 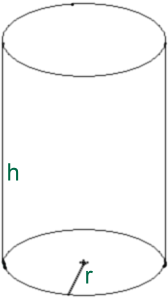
Sonderfälle:
Die Kugel (Quadratur des Kreises...HaHa): V= 4/3* pi * r³ (also etwa 4,1888 * r³)
Der Kegel: V=1/3 G * h (allgemein) 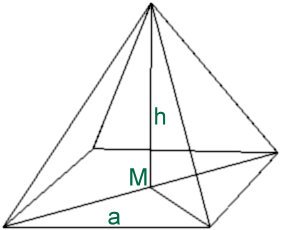
Der senkrechte Kreiskegel: V= pi /3 r² * h 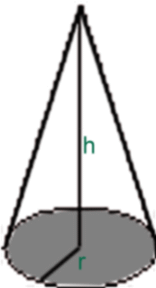
Der Kegelstumpf vom senkr. Kreiskegel: V= pi/3 * h' * (r1² + r1 r2 + r2²)
Der Pyramiden-/Kegelstumpf V=h/3 (G1 + Ö G1G2 + G2)
Zeichnungen folgen noch...
Hier gilt dasselbe, was schon bei zusammengesetzten Flächen gesagt wurde, man versucht den Körper in verschiedene, leicht(er) errechenbare Einzelkörper aufzuteilen. Deren Volumen ergeben dann in der Summe oder Differenz das Gesamtvolumen des Körpers
Ein Beispiel hierzu spare ich mir, da der Rechenweg analog zur zusammengesetzten Fläche ist
Die Rotation einer Fläche, begrenzt durch ihre Funktionslinie, errechnet durch das Integral in Bezug zu einer (Schwerpunkt)achse führt zu einem Dreh- oder Rotationskörper. Aber das gehört nun wirklich nicht mehr hierhin, da das zu weit geht. Als einfaches Beispiel sei der Ring mit Kreisförmigen Kern genannt: V=2 pi² r² R...lassen wir das.
Integral und Differentialrechnung
Keine Erläuterungen zu diesem Thema. Gesagt sei nur:
Das Integral drückt die Fläche zwischen Bezugsachse (meist X-Achse) und Funktionsgraph zwischen zwei als Start und Endpunkt genannten X-Werten aus.
Das Differential ist die Ableitung in einem Punkt auf diesem Graph der Funktion und drückt die Steigung in diesem Punkt aus.
Wer hier mehr Informationen haben möchte, der gehe bitte zur Stadtbücherei, oder frage einen Oberstufenschüler
Statistik ist die Sammlung und Auswertung von Daten, Fakten und Zahlen und ihre Umsetzung in überschaubare und leichter zu verstehende Ergebnisse. Die statistische Auswertung der gewonnenen Zahlen dient letzlich der vereinfachten Entscheidungsfindung aus den vorhandenen Werten.
Somit sind in der wirtschaftlichen Auswertung der Unternehmenszahlen Statistiken ein wirksames Mittel.
Werkzeuge und Vorgehensweisen in der Statistik
Statistik beruht auf nachgemessenen oder gesammelten Zahlen. Die Gewinnung dieser Zahlen muss, um die statistischen Grundsätze zu erfüllen, stets wiederholbar, nachvollziehbar und unabhängig erfolgen.
Diese Grundsätze sind:
Vorgänge, die zur Erstellung einer Statistik führen, müssen nach den o.g. Grundsätzen geplant und durchgeführt werden. Im Grundsatz läuft dies in vier Schritten ab: