m
2
q*p
Die Krümel KG ist ein führender Anbieter in Weinen und Spirituosen. Für das kommende Geschäftsjahr soll ein roter Bordeaux der unteren Preisklasse neu in das Sortiment aufgenommen werden. Erwartungsgemäß sollen in dieser Zeit 18.000 Flaschen abgesetzt werden. Bei einem Direktimport beträgt der Einkaufs- preis/Flasche 5 EUR. Zusätzlich verlangt der französische Erzeuger für jede Sendung eine pauschale Auslagenvergütung von 500 EUR. Die Zins- und Lagerkosten bei der KRÜMEL KG belaufen sich - auf 12 Monate gerechnet - auf 10% des Wertes der durchschnittlich eingelagerten Ware.
Soll die KRÜMEL KG ihren Gesamtbedarf von 18.000 Flaschen in Bestellmengen von 18 x 1.000, 9 x 2.000, 6 x 3.000, 3 x 6.000, 2 x 9.000 oder 1 x 18.000 Flaschen decken? Bei welcher Bestellmenge sind die Gesamtkosten für 18.000 Flaschen am geringsten, wenn alle Voraussetzungen für das Grundmodell zur Ermittlung der optimalen Bestellmenge erfüllt sind?
Es gelten die Angaben der oben aufgeführten Aufgabe. Welchen Einfluß hat eine Erhöhung des Gesamtbedarfs B, des Einstandspreises p, der bestellfixen Kosten Kf und des Lagerkostensatzes q auf die optimale Bestellmenge?
Vorraussetzung für die Anwendung der Andler - Formel
Die Gesamtkosten / Jahr setzen sich im vorliegenden Fall aus drei Bestandteilen zusammen:
| Ku = | unmittelbare Beschaffungskosten / Jahr Jahresbedarf * Preis pro ME |
B * p |
| Km = | mittelbare Beschaffungskosten / Jahr (Jahresbedarf * Bestellfixe Kosten )/Bestellmenge |
B*Kf m |
| Kl = | Lagerkosten / Jahr durchschnittlicher Bestand * Preis *Lagerzins |
B*p*q 2 |
| K = Ku + Km + Kl | Gesamtkosten =mittelbare + unmittelbare + Lagerkosten: |
Die Werte im einzelnen:
In einer Tabelle eingetragen:
| Bestellmenge | m | 1.000 | 2.000 | 3.000 | 6.000 | 9.000 | 18.000 |
| Ku = | B * p | 90.000 | 90.000 | 90.000 | 90.000 | 90.000 | 90.000 |
| Km = | Kf* B m |
9.000 | 4.500 | 3.000 | 1.500 | 1.000 | 500 |
| Kl = | m * p* q 2 |
250 | 500 | 750 | 1500 | 2250 | 4500 |
| K = | Ku + Km + Kl | 99.250 | 95.000 | 93.750 | 93.000 | 93.250 | 95.000 |
Mit 93.000 EUR erreichen die Gesamtkosten ihren niedrigsten Wert,wenn der Gesamtbedarf in dreiBeschaffungsvorgängen mit einer Bestellmenge von jeweils 6.000 Flaschen gedeckt wird. Die optimale Bestellmenge m(opt) beträgt somit 6.000 Flaschen. Die mathematische Betrachtung der Werte ergibt, dass die unmittelbaren Kosten der Beschaffung, also Ku, stets den gleichen Wert von EUR 90000,- hat. Variabel hingegen entwickeln sich Kl (Lagerkosten) und Km (mittelbare Bestellkosten).
Auf die optimale Bestellmenge haben also nur die mittelbaren Beschaffungskosten Km und die Lagerkosten Kl Einfluß. Die unmittelbaren Beschaffungskosten Ku spielen keine Rolle, weil sie von der Bestellmenge unabhängig sind. Im einzelnen beeinflussen die verschiedenen Komponenten die optimale Bestellmenge wie folgt:
Gesamtbedarf B
Eine Erhöhung ( Verringerung ) des Gesamtbedarfs bewirkt eine Vergrößerung ( Verringerung )
der optimalen Bestellmenge, weil die mittelbaren Beschaffungskosten Km, die für eine möglichst
große Bestellmenge sprechen, durch eine Erhöhung des Gesamtbedarfs ein stärkeres Gewicht
erhalten.
Einstandspreis p
Durch Erhöhung(Verringerung) des Einstandspreises p steigen(fallen) die Lagerkosten Kl, weil
der Wert des durchschnittlichen Lagerbestandes zunimmt(abnimmt). Durch einen höheren
Einstandspreis erhalten die Lagerkosten, die für eine möglichst geringe Bestellmenge sprechen,
ein stärkeres Gewicht. Bei Erhöhung(Verringerung) des Einstandspreises p fällt(steigt) der
optimalen Bestellmenge.
Bestellfixe Kosten K
Durch einen Anstieg der bestellfixen Kosten Kl erhöhen sich die mittelbaren Beschaffungs-
kosten Km. Da die mittelbaren Beschaffungskosten für möglichst große Bestellmengen
sprechen, erhöht(verringert) sich die optimale Bestellmenge infolge gestiegener(gefallener)
bestellfixer Kosten.
Lagerkostensatz q
Größere Bestellmengen sind mit höheren Lagerkosten Kl verbunden. Wenn sich der
Lagerkostensatz erhöht, ist es vorteilhaft, den stärker ins Gewicht fallenden Lagerkosten
durch Verringerung der Bestellmenge auszuweichen.
Die gewonnene Erkenntniss, daß nur die mittelbaren Kosten sowie die Lagerkosten auf die Höhe der optimalen Bestellmenge Auswirkungen haben, und die Begebenheit, daß im Bestelloptimum die Km gleich der Kl sind, da nach Gleichsetzungsverfahren der Schittpunk beider Funktionen den kleinsten geimeinsamen Wert bilden, läßt die Anwendung der " Ander - Formel " zu:
| Km = Kl; | Km= Kf*B m | Kl=q*p*m 2 |
| => | Kf * B m |
= | q*p*m 2 |
| <=> | Kf * B *2 | = | q*p*m*m |
| <=> | Kf * B *2 q*p |
= | m² |
| <=> | = | m |
Diese Formel nennen wir die Ander´sche Formel für die optimale Bestellmenge Xopt. Diese Formel ist in zwei Variationen in der Literatur zu finden:
| oder |
Das rührt daher, dass im Ersten fall die Lagerzinsen q als Faktor von 100 (z.B: 0,15), im zweiten Fall als Prozentsatz (z.B.: 15%) angesetzt werden.
Optimale Beschaffungsmenge X opt.
Wie bnereits gesehen setzt die Ander-Formel den Bezug zwischen Lagerhaltungskosten, Zinsen für das eingelagerte Material, die Stückkosten mit Mengenrabatten und die Beschaffungsfixkosten( z.B.: Porto, Versand und Verpackung) und den Jahresbedarf zueinander in Relation, um aus diesen Werten die kostengünstigste Bestellmenge und -häufigkeit herauszufinden.
Beispiel:
Das Unternehmen hat mittelbare Beschaffungskosten von EUR 30,- ; Lagerhaltungskostensatz ist 15%; der Gesamtbedarf liegt bei 1250 ME / anno, der Einführungspreis pro ME beträgt EUR 20,-
Ermitteln Sie:
Die Ander`schen Formel für die
optimale
Beschaffung /-Bestellmenge :
![]()
Hierbei sind:
Die Beschaffungshäufigkeit ermittelt sich, indem der
Jahresbedarf durch die gleichbleibende Bestellmenge geteilt wird.
Somit ergibt sich natürlich für Optimale Beschaffungshäufigkeit:
| B [Q] Xopt |
= NOPT | |
| => | 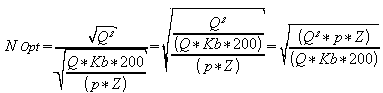 |
|
| NachKürzung ergibt sich die Formel für die optimale Beschaffungshäufigkeit: |
||
| In unserem Beispiel eingesetzt: | ||
| =7,9i.e. 8 x im Bedarfszeitraum | ||
Beschaffungsrythmus
Kaufmännische 360 Tage geteilt durch Häufigkeit der Bestellung:
360 / N opt. = 360 : 8 = 45 Tage
Kosten pro Stück
Aus der optimalen Bestellmenge und der Bedarfsmenge kann bei abweichender Bestellmenge oder variablen Jahresbedarfsmengen Rückschluß auf die Tatsächlichen Kosten gezogen werden
Die Formel hierfür lautet:![]()
Hierbei ist Q = Bedarf, X opt. = optimale Bestellmenge, p = Einstandspreis, Z = Lagerzinssatz, Kb = Bestellkosten pro Bestellung